إذا كانت ٣ × ٥ = ١٥ فإن ٥ × ٣ = ١٢

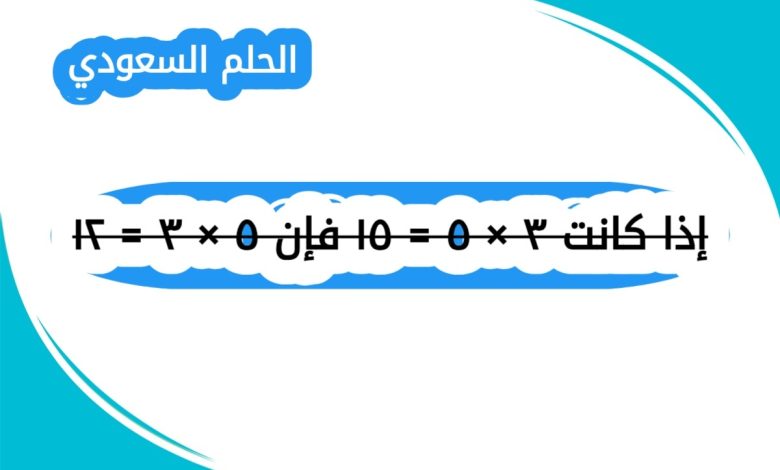
إذا كانت ٣ × ٥ = ١٥ فإن ٥ × ٣ = ١٢؟ فهم العمليات الحسابية الأساسية من اهم المهارات الرياضية التي يحتاجها الطلاب والاجابة على السؤال هي خطأ. عملية الضرب تمتاز بخاصية التبادلية، مما يعني ان ترتيب الاعداد في الضرب لا يؤثر على الناتج. فاذا كانت ٣ × ٥ = ١٥، فإن ٥ × ٣ ايضا تساوي ١٥، وليس ١٢ كما ذكر في السؤال. هذه الخاصية تساعد على تبسيط العمليات الحسابية وفهم العلاقة بين العوامل والناتج.

تطبيق خاصية التبادلية في الضرب مهم في حل المسائل الرياضية اليومية، مثل حساب المساحات، الكميات، والمبالغ المالية. ايضا، تعتبر هذه القاعدة الاساسية جزءاً من تعلم الجبر والمفاهيم الرياضية الاكثر تعقيداً في المراحل الدراسية المتقدمة. الطلاب الذين يفهمون هذه القاعدة يكونون اكثر قدرة على حل المسائل بسرعة ودقة.

مثال عملي: اذا كان لديك ٣ صفوف من الكراسي كل صف يحتوي على ٥ كراسي، يمكنك بسهولة حساب العدد الاجمالي للكراسي بضرب ٣ × ٥ = ١٥. وبنفس الطريقة، لو عكسنا الاعداد ٥ × ٣ فان الناتج يظل ١٥، مما يؤكد ان ترتيب الاعداد في الضرب لا يغير الناتج. هذه الخاصية تتيح ايضاً تسهيل العمليات الحسابية الكبيرة وتقليل الاخطاء عند التعامل مع الارقام.

من الامور المهمة في تعلم الرياضيات هو التأكد من صحة الاجابات وعدم الاعتماد على التخمين. خاصية التبادلية في الضرب من اهم القواعد التي تساعد الطلاب على تطوير مهاراتهم الحسابية والتفكير المنطقي. ايضا، تساعد هذه القاعدة على فهم العمليات الاخرى مثل الجمع، الطرح، والقسمة بطريقة اسرع واسهل.

باختصار، اذا كانت ٣ × ٥ = ١٥ فان ٥ × ٣ ايضا = ١٥ وليس ١٢. فهم خصائص العمليات الحسابية الاساسية مثل التبادلية في الضرب يعزز الدقة والمهارة في الرياضيات، ويساعد على حل المسائل اليومية والتعليمية بكفاءة عالية.