
عدد رؤوس متوازي المستطيلات: شرح مبسط ومعلومات هامة، يعد متوازي المستطيلات أحد الأشكال الهندسية ثلاثية الأبعاد الأساسية التي تُدرَّس في المناهج الدراسية بمختلف المراحل، ويكثر البحث حول خصائصه، لا سيما عدد رؤوسه. في هذا المقال من موقع الحلم السعودي، سنتعرف على عدد رؤوس متوازي المستطيلات بشكل مبسط، بالإضافة إلى استعراض خصائصه الهندسية المهمة وأهميته في حياتنا اليومية.
ما هو متوازي المستطيلات
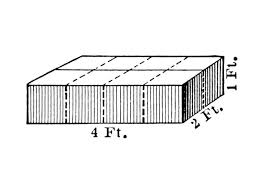
متوازي المستطيلات (Rectangular Prism) هو شكل هندسي ثلاثي الأبعاد يتكون من 6 وجوه، جميعها مستطيلات، و12 ضلعًا، و8 رؤوس. يتميز بأن جميع زواياه قائمة (90 درجة)، وتكون أضلاعه المتقابلة متساوية في الطول.
عدد رؤوس متوازي المستطيلات

حل سؤال عدد رؤوس متوازي المستطيلات هو 8 رؤوس. هذه الرؤوس هي نقاط التقاء ثلاثة أضلاع في كل زاوية من زوايا الشكل، وتُمثل الزوايا الخارجية له. وتظهر هذه الرؤوس بوضوح عند رسم النموذج ثلاثي الأبعاد أو عند استخدام مكعب أو صندوق كأداة تعليمية.
خصائص متوازي المستطيلات
- عدد الأوجه: 6 أوجه، وكل وجه على شكل مستطيل.
- عدد الأضلاع: 12 ضلعًا.
- عدد الرؤوس: 8 رؤوس.
- الزوايا: 90 درجة في كل زاوية، مما يجعله شكلًا قائم الزوايا.
- الحجم: يحسب من خلال العلاقة:
أهمية معرفة عدد رؤوس متوازي المستطيلات
فهم خصائص متوازي المستطيلات مثل عدد الرؤوس يُساعد الطلاب والمهتمين بالرياضيات والهندسة في تحليل الأشكال الهندسية والتعامل معها في المسائل الحسابية أو التصميمات الهندسية، وهو ما يجعلها جزءًا أساسيًا من التعليم.
أمثلة على متوازي المستطيلات في حياتنا
- الصناديق الكرتونية.
- الثلاجات.
- قطع الأثاث (مثل الطاولات والمكاتب).
- الكتب المغلقة.
- حقائب السفر.
نهاية المقال
عدد رؤوس متوازي المستطيلات هو 8 رؤوس، ويُعتبر هذا الشكل من أكثر الأشكال شيوعًا في الدراسة والتطبيقات العملية. يساعدنا فهم خصائصه في الكثير من المجالات التعليمية والعملية، كما يُمثل أساسًا هامًا في الهندسة الفراغية.
